Hello World

Before starting, let’s make sure we have the right libraries installed.

$pip install torch matplotlib numpy pandas torchvision torchaudio

Then, import the right libraries and select a device for running accelerated PyTorch code.

import pandas as pd
import numpy as np
import torch 
from torch import nn
from torch.utils.data import DataLoader, Dataset
from torchvision.transforms import ToTensor
import matplotlib.pyplot as plt
from os import path

device = (
    "cuda"
    if torch.cuda.is_available()
    else "mps"
    if torch.backends.mps.is_available()
    else "cpu"
)

print(device)

In my case, the device will be mps, as I am running this on a MacBook Pro M1 Max.

Loading and processing the data

For this example I will use the Jena Climate dataset and the goal will be to predict the temperature (Celsius) over the future 1 or more hours. We are going to use 4 different approaches, a basic linear regression, a simple neural network, a convolutional neural network and, then, a recurrent neural network. They all give pretty good results and we will discuss the differences throughout the post.

Unlike in the TensorFlow tutorial on which this code is based, I will remove the temperature-related features from the training data and only keep them in the target variable. As such, we make the work of the ML models a bit harder.

The first step is loading the data and separating the date_time variable. We will process the date_time a bit later to include it back in the trianing set.

# df contains hourly data
df = pd.read_csv("jena_climate_2009_2016.csv")[5::6]
date_time = pd.to_datetime(df.pop('Date Time'), format='%d.%m.%Y %H:%M:%S')
df.head()

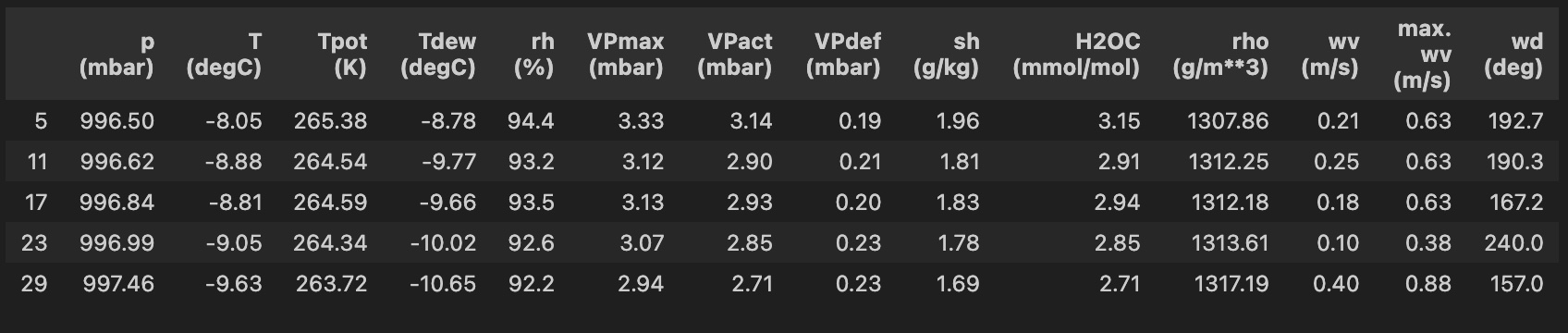
Next, we are going to do a bit of data cleanup and transform some of the variables:

• Ensure there is no windspeed lower than 0
• Convert wind direction from degrees to vectors (maintaining magnitude)
• Standardize all numeric features for better processing by the neural networks
• Validate the periodicity of the time signal and transform from date_time to continuous variables that can be used in training.

One by one, in the order specified above.

df['wv (m/s)'][df['wv (m/s)'] < 0] = 0
df['max. wv (m/s)'][df['max. wv (m/s)'] < 0] = 0
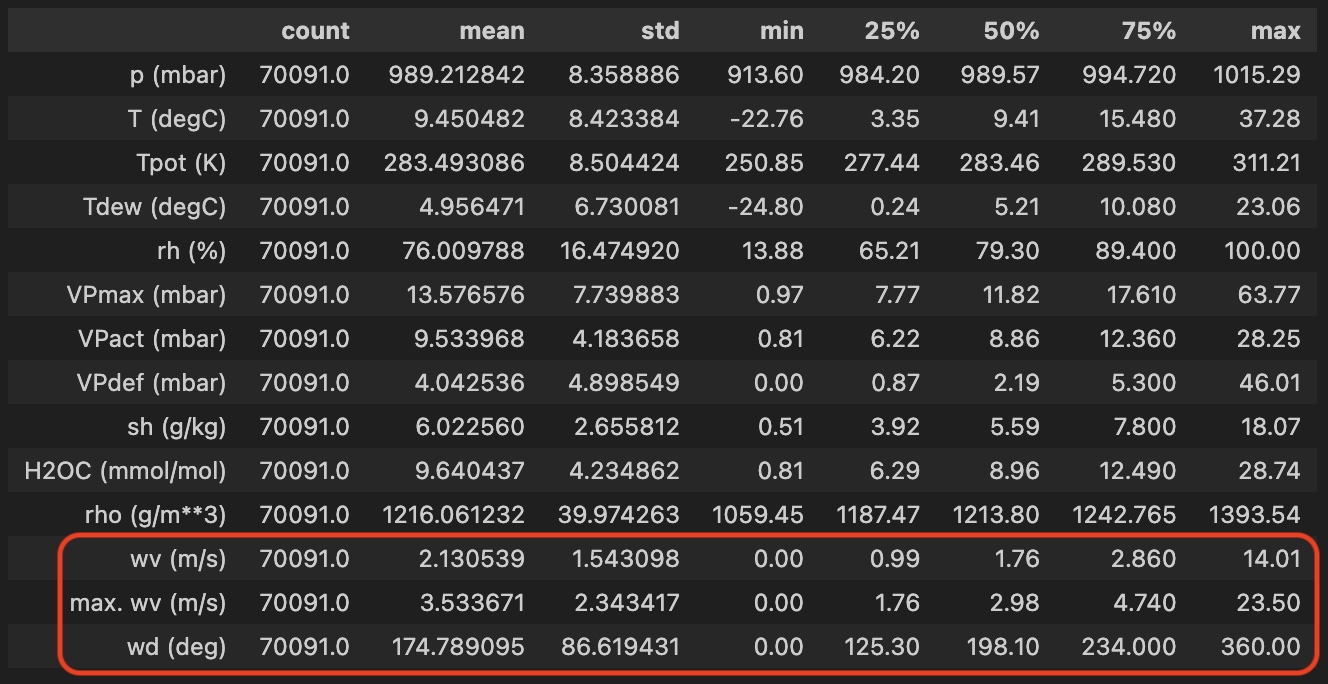
df.describe().transpose()

# convert the wind degrees and wind speed to a wind vector
wv = df.pop('wv (m/s)')
max_wv = df.pop('max. wv (m/s)')

# Convert to radians.
wd_rad = df.pop('wd (deg)')*np.pi / 180

# Calculate the wind x and y components.
df['Wx'] = wv*np.cos(wd_rad)
df['Wy'] = wv*np.sin(wd_rad)

# Calculate the max wind x and y components.
df['max Wx'] = max_wv*np.cos(wd_rad)
df['max Wy'] = max_wv*np.sin(wd_rad)

# show wind vectors looking great
plt.hist2d(df['Wx'], df['Wy'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind X [m/s]')
plt.ylabel('Wind Y [m/s]')
ax = plt.gca()
ax.axis('tight')

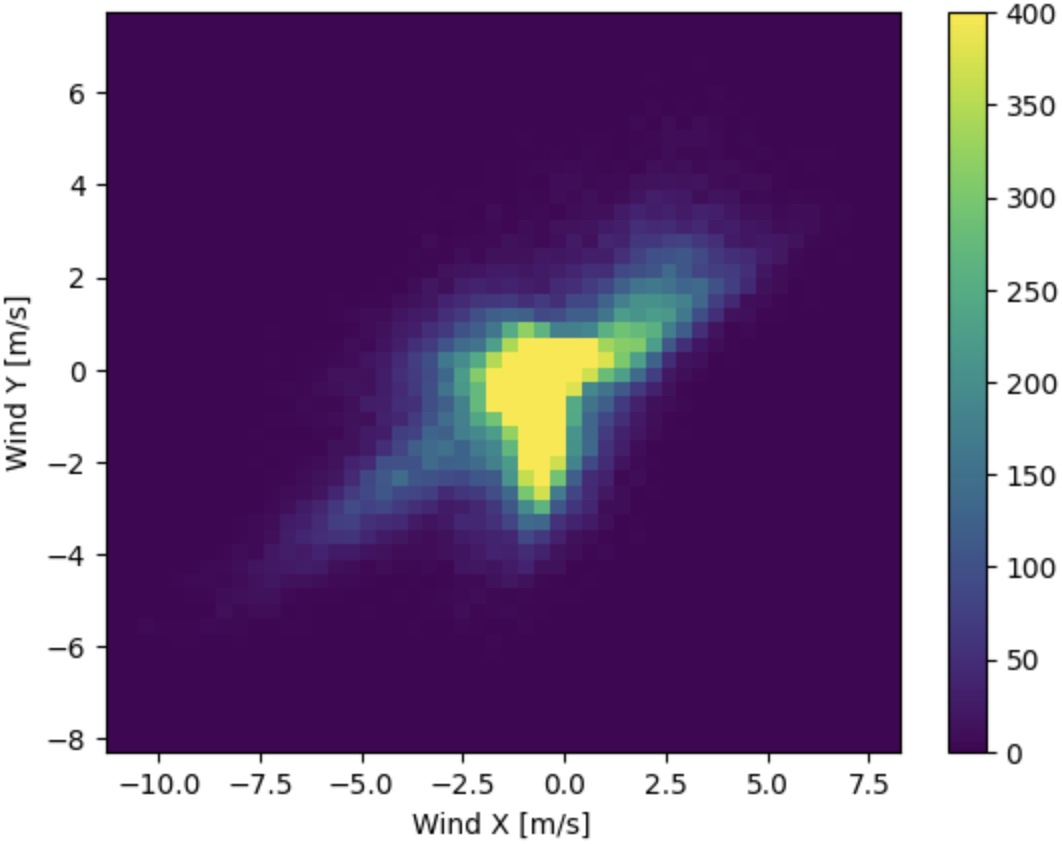
Nothing fancy so far, just similar procesing as in the TensorFlow tutorial.

# standardize all numeric features
df = (df-df.mean(axis=0)) / df.std(axis=0)
df["T (degC)"].plot()
df["p (mbar)"].plot()

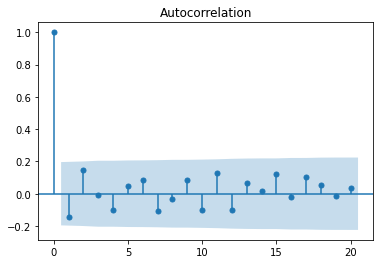
The following snippet of code is slightly more intersting. While in this case our intuition tells us that we have yearly and daily periodicity, the safest way to approach the problem of timeseries is to validate. We are going to analyse the spectrum of the signal and confirm our intuition. Comments inline, in the code.

# check for seasonality
from collections import defaultdict

# confirm the data is sampled hourly
print(date_time[0:10])

# compute the fast fourier transform of the temperature
temp = np.array(df["T (degC)"])
fft = np.fft.fft(temp)

N = len(temp) # length
T = 1 # sample frequency, 1/hour
D = N * T # duration
# the following line computes the actual frequencies in the spectrum
frequency = np.fft.fftfreq(N, d=T)

# we are interested only in the first half of the array
# the second half is filled with the conjugates for the first half
fft = fft[:int(N/2)]
frequency = frequency[:int(N/2)]

# take the highest 10 frequencies and compute their amplitude
max = np.abs(fft).argsort()[::-1][:10]

# compute the lengh of the period (1/freq) an the magnitudes
periods = (1.0 / frequency[max]) / 24 # 24 == convert from hours to days
magnitudes = np.abs(fft[max]) * 2 / N

# sampling is not perfect, hence some of the frequencies may fall in 
# two different buckets: e.g. 0.99h and 1.01h
cnt = defaultdict(lambda: 0)
for k, v in zip([str(int(x+0.1)) for x in periods], magnitudes):
    cnt[k] += v

# plot the frequencies and their magnitude
plt.bar(cnt.keys(), cnt.values())

# we see clearly there is a yearly fundamental and a daily fundamental 
# (2920 days == 8 years - the number of years we have data for)

Periods in days - outstanding at 365 days and 1 day, as expected:

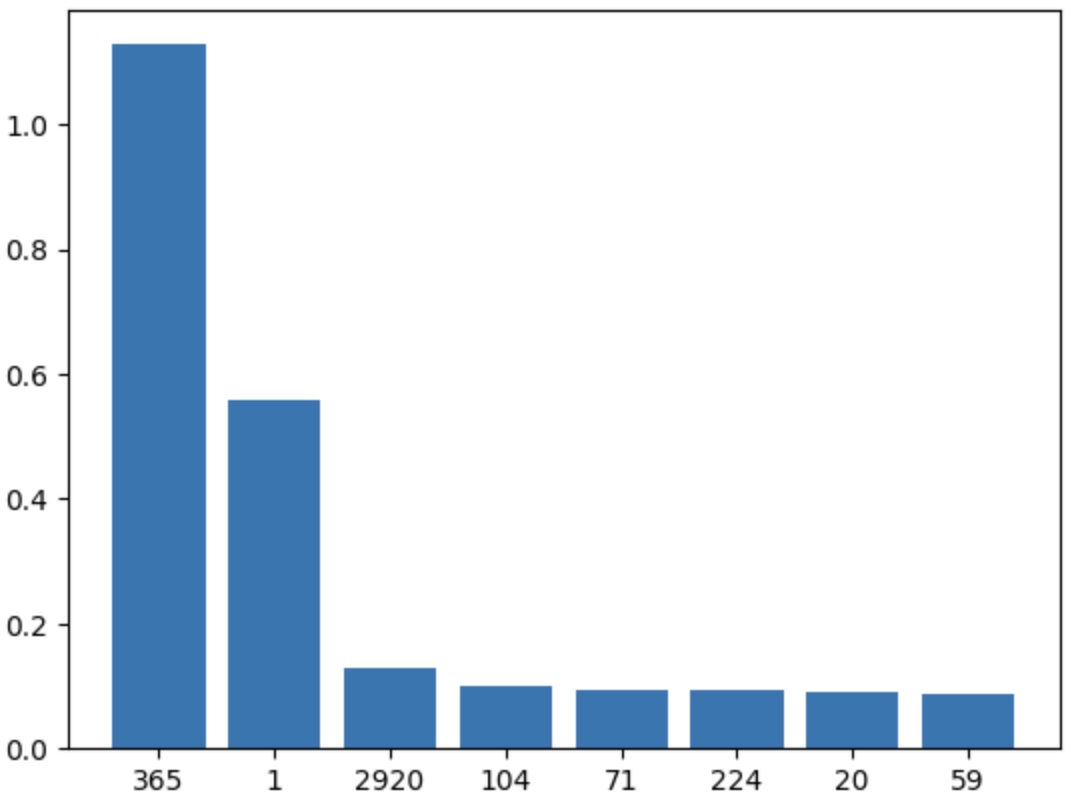
Given the information above, we can safely encode time as sin and cos for two different periods - yearly and daily. We are using both sin and cos in order to not confuse the algorithm as each sin and cos cross the 0 axis twice, having twice the same values over a period.

timestamp_s = date_time.map(pd.Timestamp.timestamp)

day = 24*60*60
year = (365.2425)*day # a bit of correction

# normalized already
df['Day sin'] = np.sin(timestamp_s * (2 * np.pi / day)) * 0.5
df['Day cos'] = np.cos(timestamp_s * (2 * np.pi / day)) * 0.5
df['Year sin'] = np.sin(timestamp_s * (2 * np.pi / year)) * 0.5
df['Year cos'] = np.cos(timestamp_s * (2 * np.pi / year)) * 0.5

Generating the datasets

After ensuring we have clean data, we are going to generate 3 data splits: training, validation and test.

# timeseries, so no random split
train_df = df[ : int(0.7 * len(df))]
val_df = df[int(0.7 * len(df)) : int(0.9 * len(df))]
test_df = df[int(0.9 * len(df)) : ]

In PyTorch, data is fed to the training loop through a DataLoader object. It handles batching and shuffling, and wraps a user-defined Dataset. The Dataset object needs to implement the standard __len__ and __getitem__ functions, so it behaves like an array.

For our code, we will implement a custom Dataset which wraps a Pandas dataframe and returns a specified number of time points as features and another number of time points as targets. In addition, it will have plotting functions for easier debugging and vizualization.

The parameters for the Dataset construction are as follows:

• df - the Pandas dataframe to wrap
• input_window_len - how many past points of time (hours in our case) to return as features
• target_len - how many points in the future to return as target, for one-shot predictions
• shift - when moving through the dataset, by how many datapoints to advance the cursor,
• var_columns - which columns to include in the features
• target_columns - which columns to include in the target
• transform and target_transform - how to transform the resulting data, in our case it will be transformed to a torch.Tensor and dispatched to the GPU.

One thing to note is to never-ever use Pandas in the training loop as it will slowdown training by at least 100x. Only use numpy arrays and do the conversion outside of the __getitem__ function. We do this update in the preprocess method of the class.

class WindowedDataset(Dataset):
    
    def __init__(self, df,  
                        input_window_len, 
                        target_len, shift, v
                        ar_columns, target_columns, 
                        transform=None, 
                        target_transform=None) :
        super().__init__()

        self.df = df
        self.input_window_len = input_window_len
        self.target_len = target_len
        self.shift = shift
        self.transform = transform
        self.target_transform = target_transform
        self.target_columns = target_columns
        self.var_columns = var_columns

        self.precompute()

    def get_input_size(self):
        return self.input_window_len * len(self.var_columns)
    
    def get_target_size(self):
        return self.target_len * len(self.target_columns)
    
    def count_channels(self):
        return len(self.var_columns)

    def __len__(self):
        return int((len(self.df) - self.target_len - self.input_window_len) / self.shift)
    
    def precompute(self):
        self.variables_ = np.array(self.df[self.var_columns])
        self.target_ = np.array(self.df[self.target_columns])
    
    def __getitem__(self, idx):
        start = idx * self.shift

        variables = self.variables_[start : start + self.input_window_len]
        variables = variables.flatten()
        
        target = self.target_[start + self.input_window_len : start + self.input_window_len + self.target_len]
        target = target.flatten()

        if self.transform:
            variables = self.transform(variables)
        if self.target_transform:
            target = self.target_transform(target)

        return variables, target
    
    def plot(self, idx, col_name):
        if not hasattr(idx, '__iter__'):
            idx = [idx]
        else:
            idx = list(idx)
        try: 
            var_tmp = self.var_columns
            target_tmp = self.target_columns

            self.var_columns = [col_name]
            self.target_columns = [col_name]
            self.precompute()

            cnt = self.input_window_len + self.target_len + (len(idx) - 1) * self.shift
            v = [0] * (self.input_window_len + (len(idx) - 1) * self.shift)
            t = [0] * (self.target_len + (len(idx) - 1) * self.shift)

            start = idx[0] * self.shift

            for i in idx:
                v_, t_ = self[i]

                ii = (i - start) * self.shift
                v [ii : ii + len(v_)] = v_ 
                t [ii : ii + len(t_)] = t_

            axis = range(start, start + cnt)
            plt.plot(axis[0 : len(v)], v)
            plt.scatter(axis[self.input_window_len : cnt], t)

            return axis, start, cnt
        
        except Exception as e:
            raise e
        finally:
            self.var_columns = var_tmp
            self.target_columns = target_tmp
            self.precompute()

    
    def plot_prediction(self, idx, col_name, model):
        if not hasattr(idx, '__iter__'):
            idx = [idx]

        axis, start, cnt = self.plot(idx, col_name=col_name)

        with torch.no_grad():
            preds = []
            # slow way to infer
            for i in idx:
                X, _ = self[i]
                X = X[None, :] # add batch dimension
                X = X.to(device)
                y = model(X).item()

                if hasattr(y, "__iter__"):
                    preds += list(y)
                else:
                    preds.append(y)

            plt.scatter(axis[cnt - len(preds) : cnt], preds)
            plt.show()

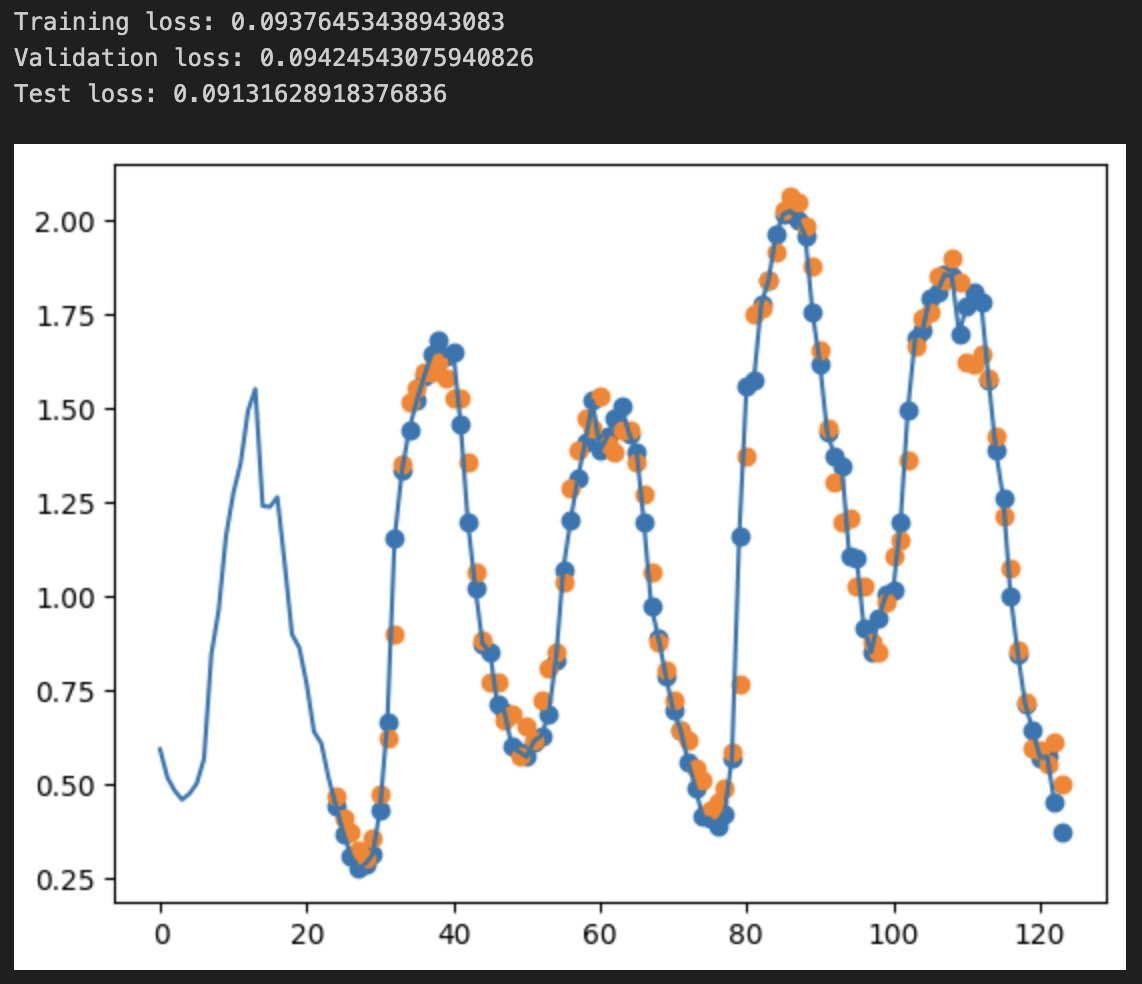
Let’s test the WindowedDataset and ask it to plot something.

# build a test dataset based on train_df
# return 100 points for each index
# return 10 points for each target
# advance by 1
wds = WindowedDataset(train_df, 100, 10, 1, df.columns, "T (degC)" )

# print the last object from the set
print(wds[len(wds) - 1])

# plot the series starting at index 10
# and use only the temperature
# the feature will be plotted with continuous line
# the target with dots
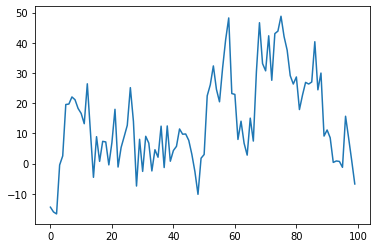
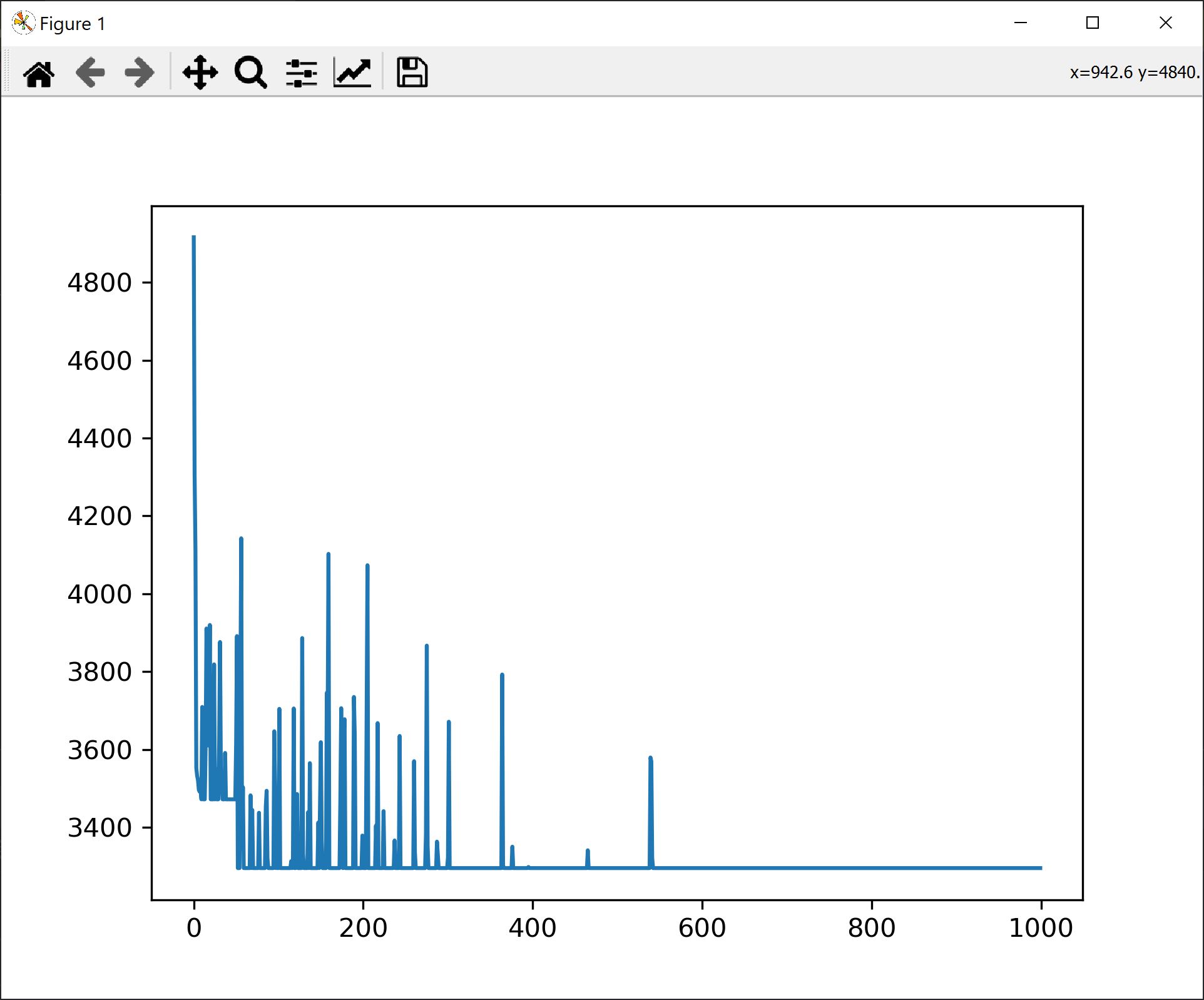
wds.plot(10, "T (degC)")

And the result of the plot - 100 points for the features, only the degrees Celsius (continous line) and the target, 10 points, as dots. The X-axis starts from 10 (starting index) to 120 (10 + 100 + 10).

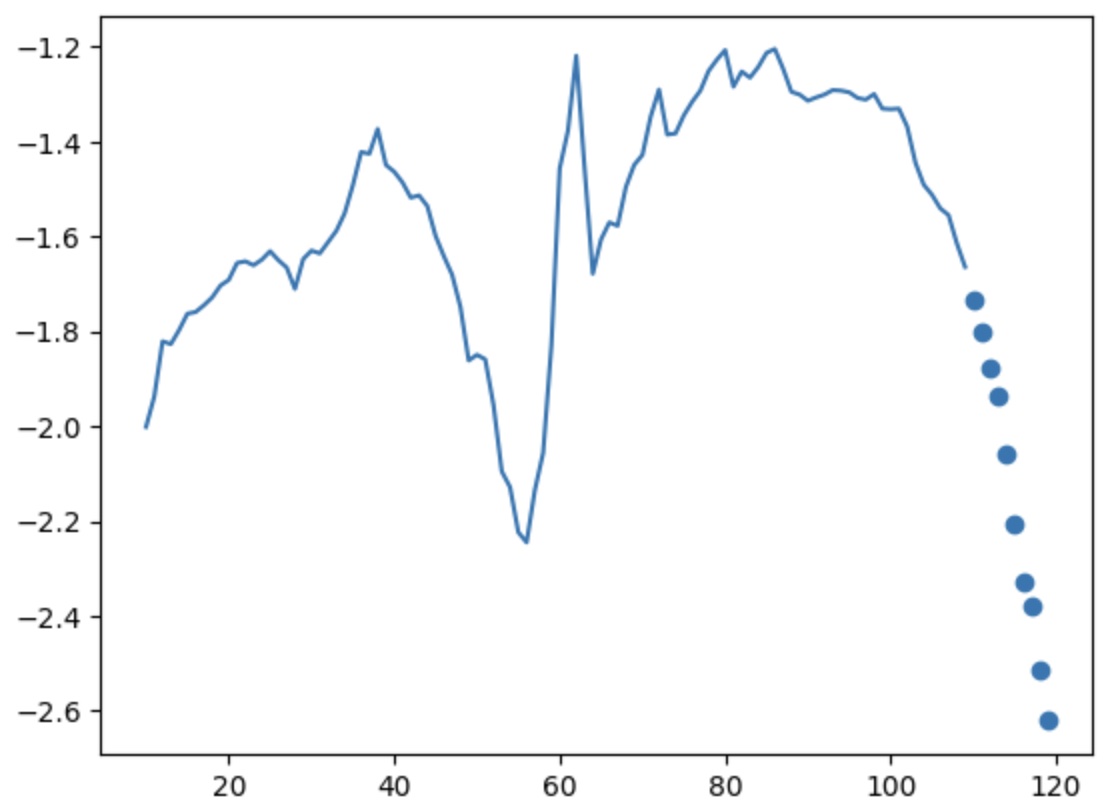
We finish this part of data preparation and dataset construction by presenting the functions that construct 3 Dataloader objects for train, validation and test respectively. To note the transform lambda which transforms from numpy to a torch.Tensor of float32.

def make_dataloader(df, input_window_len, target_len, shift):
    cols = list(df.columns)

    # make it a bit more complicated, remove the temperature completely
    # usually this is not needed for timeseries prediction
    # but more interesting to see how the models behave
    cols.remove("T (degC)")
    cols.remove("Tpot (K)")
    cols.remove("Tdew (degC)")
    
    print(cols)
    return DataLoader(
        WindowedDataset(
            df, input_window_len, target_len, shift, cols, ["T (degC)"],  
            transform=lambda v: torch.tensor(v, dtype=torch.float32),
            target_transform= lambda v: torch.tensor(v, dtype=torch.float32)
        ), 
        batch_size=128, 
        shuffle=True)

def make_loaders(input_window_len, target_len, shift):
    train_loader = make_dataloader(train_df, input_window_len, target_len, shift)
    valid_loader = make_dataloader(val_df, input_window_len, target_len, shift)
    test_loader = make_dataloader(test_df, input_window_len, target_len, shift)

    return train_loader, valid_loader, test_loader

Training loop and evaluating

PyTorch uses Autograd and a pretty straightforward training loop. To note are:

• Transferring the tensors to the GPU with the .to(device) calls.
• Defining a custom loss (RMSELoss)
• with torch.not_grad() when making predictions
• How backpropagation is implemented and using the optimizer
• Saving and loading a model

def RMSELoss(yhat,y):
    return torch.sqrt(torch.mean((yhat-y)**2))

def eval_(model, dl):
    res = []
    with torch.no_grad():
        for batch, (X, y) in enumerate(dl):
            X, y = X.to(device), y.to(device)
            pred = model(X)
            res.append(RMSELoss(y, pred).item())

            # take only the first 20 batches top
            if batch > 20:
                break

    return np.mean(res)

def eval(model, train_ds, valid_ds, test_ds):
    print("Training loss:", eval_(model, dl=train_ds))
    print("Validation loss:", eval_(model, dl=valid_ds))
    print("Test loss:", eval_(model, dl=test_ds))

def create_trainer(dataloader, model, epochs):
    try:
        torch._dynamo.config.suppress_errors = True
        model = torch.compile(model)
    except:
        print ("torch.compile() not available.")

    losses = []
    m = model
    
    loss_fn = RMSELoss
    optimizer = torch.optim.Adam(model.parameters(), lr=2e-4)

    def train():
        # loop through the dataset and perform backpropagation"

        size = len(dataloader.dataset)
        model.train()

        for batch, (X, y) in enumerate(dataloader):
            X, y = X.to(device), y.to(device)

            # Compute prediction error
            pred = model(X)
            loss = loss_fn(pred, y)

            # Backpropagation
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

            # save losses for plotting
            losses.append(loss.item())

            if batch % 100 == 0:
                loss, current = loss.item(), (batch + 1) * len(X)
                print(f"loss: {loss:>7f}  [{current:>5d}/{size:>5d}]")

    def trainer():
        # load a model if already exists
        # else loop (epochs) times through the train function

        model_str = str(m)
        model_str = ''.join([s for s in model_str if s.isalnum()])
        model_str = model_str[0 : min(150, len(model_str))]

        if path.exists(model_str):
            return torch.load(model_str)
        else:
            for i in range(epochs):
                print("Epoch ", i)
                train()
            plt.plot(losses)
            plt.show()
            torch.save(m, model_str)
            return m

    return trainer

Basic Linear Regression

The simplest model will take the atmospheric parameters for one hour and predicts the temperature for the next hour. It’s a basic neural network with 1 neuron and no activation, equivalent to a simple linear regression.

The interesting things to note are:

• The structure of a neural network in PyTorch, inheriting from the nn.Module base class
• The forward() function which performs the forward propagation and evalution step
• The use of an nn.Linear object which is the equivalent of a Dense layer
• The use of .to(device) to ensure all parameters are submitted to the GPU

class BasicLinear(nn.Module):
    def __init__(self, input_size, target_size):
        super().__init__()
        self.linear_stack = nn.Sequential(
            nn.Linear(input_size, target_size),
        )

    def forward(self, x):
        return self.linear_stack(x)

# one hour of data and predict the following hour
t, v, tt = make_loaders(1, 1, 1)
model = BasicLinear(t.dataset.get_input_size(), t.dataset.get_target_size()).to(device)
print(model)

As a side note, if I were to build a custom linear layer, CustomDense, which does exactly the same thing as the nn.Linear, it would be as follows. Please note the use of nn.Parameter() to allow the system to keep track of the trainable weights.

class CustomDense(nn.Module):

    def __init__(self, size_in, size_out):
        super().__init__()

        #1. Explicit what is trainable parameters
        # nn.Parameter - trainable parameters
        # it's what we send to the constructor of the Optimizier.
        self.weights = nn.Parameter(
            torch.Tensor(size_out, size_in)
        )  

        self.bias = nn.Parameter(
            torch.Tensor(size_out)
        ) 

        #2. Initialize weights and biases
        # He initialization
        nn.init.kaiming_uniform_(self.weights, a=np.sqrt(5))
        nn.init.uniform_(self.bias, -0.1, 0.1)

    def forward(self, x):
        # w times x + b
        w_times_x= torch.mm(x, self.weights.t())
        return torch.add(w_times_x, self.bias)

Now let’s use the basic network above.

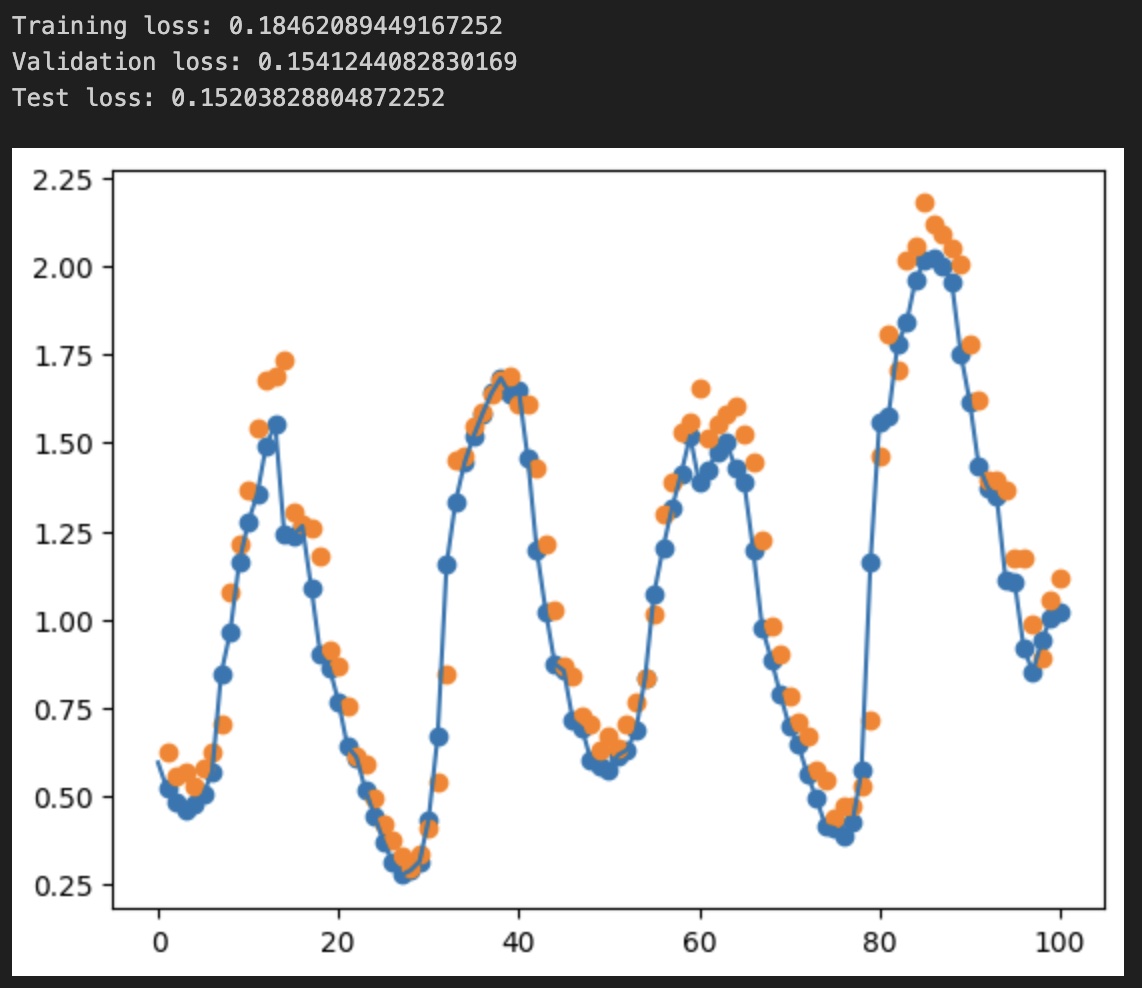
# train for 5 epochs
model = create_trainer(t, model, 5)()
eval(model, t, v, tt)

# plot the temperature - actual: blue dots, predicted: organge dots
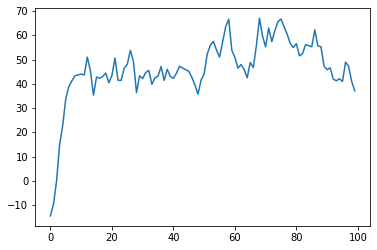
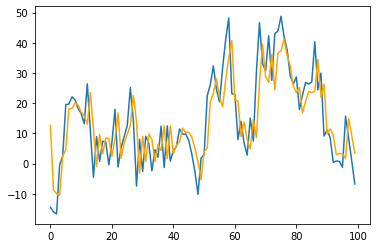
v.dataset.plot_prediction(range(0, 100), "T (degC)", model)

We observe the loss values for all sets, showing we don’t overfit but also not fit too well the data.

Deep Neural Network

We are going to proceed similarly as before but add more neurons to the mix. We now send 24h of data to predict 1h in advance. The code can be changed to predict as many hours as we want in advance, buy changing only the second parameter in the make_loaders(24, 1, 1) call.

# deep learning, dense, given 24h of data, predict 1h in advance,
class DNNRegressor(nn.Module):
    def __init__(self, input_size, target_size):
        super().__init__()
        self.linear_stack = nn.Sequential(
            nn.Linear(input_size, input_size),
            nn.ReLU(),
            nn.Linear(input_size, 64),
            #nn.Dropout(p=0.2),
            nn.ReLU(),
            nn.Linear(64, 64),
            nn.ReLU(),
            nn.Linear(64, target_size)
        )

    def forward(self, x):
        return self.linear_stack(x)
    
t, v, tt = make_loaders(24, 1, 1)
model = DNNRegressor(t.dataset.get_input_size(), t.dataset.get_target_size()).to(device)
print(model)
print("Total params: ", sum(p.numel() for p in model.parameters() if p.requires_grad))

With the model structure and number of parameters:

DNNRegressor(
  (linear_stack): Sequential(
    (0): Linear(in_features=384, out_features=384, bias=True)
    (1): ReLU()
    (2): Linear(in_features=384, out_features=64, bias=True)
    (3): ReLU()
    (4): Linear(in_features=64, out_features=64, bias=True)
    (5): ReLU()
    (6): Linear(in_features=64, out_features=1, bias=True)
  )
)
Total params:  176705

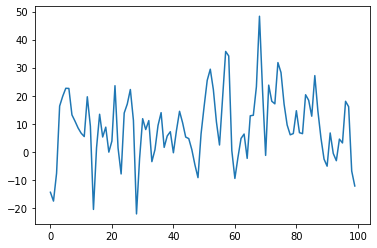
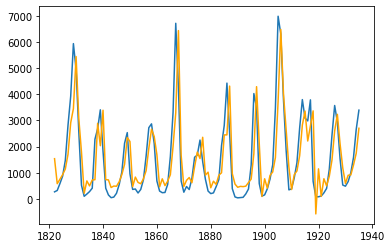
The results are as follows, and we immediately notice the lower loss while still not overfitting the dataset. Also visually, the predictions look more precise than in the linear regression case, which is expected.

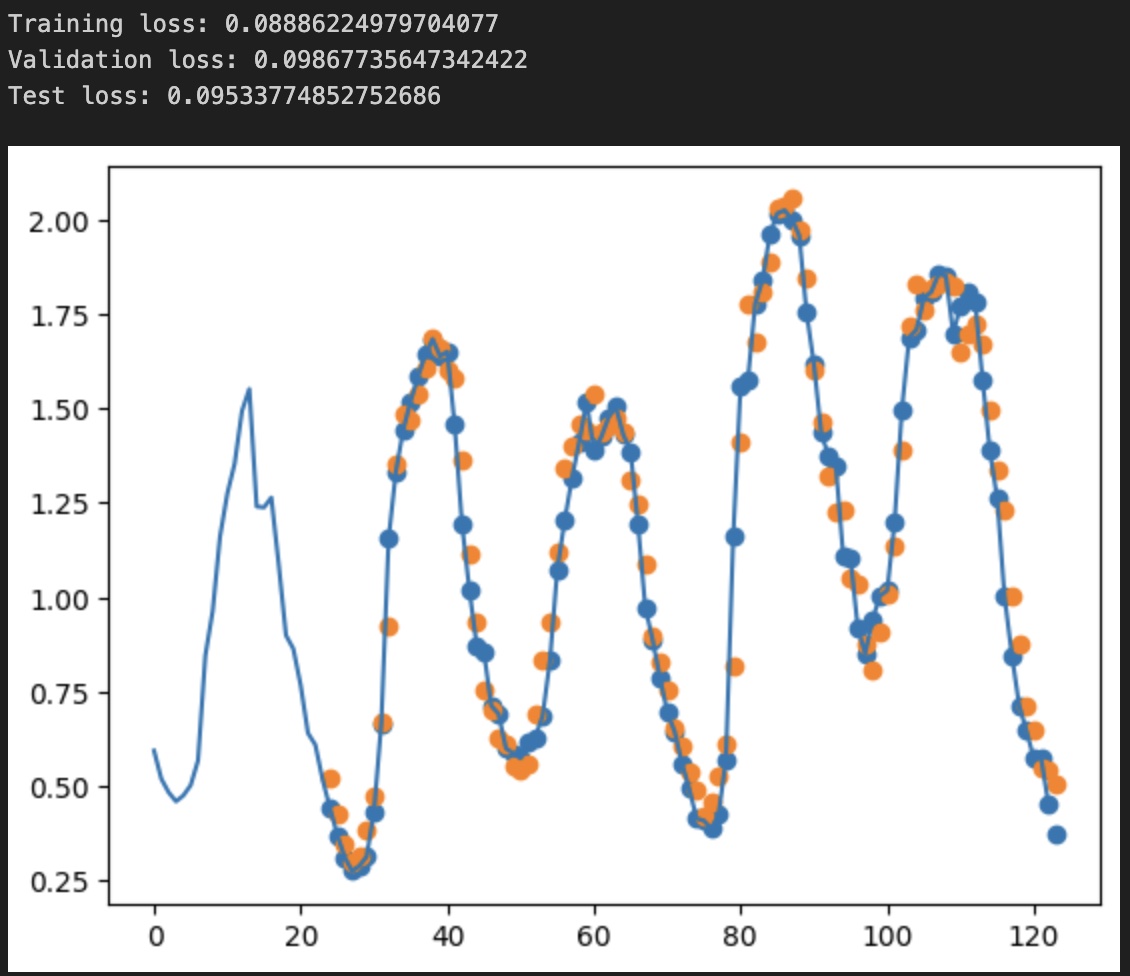
Convolutional Neural Network

We are now going to replace one of the dense layers above with a convolutional layer. CNNs tend to have less parameters than basic DNNs due to the locality of the convolutional transform. They also tend to incorporate better local relationships in the data and extract patterns. This is why they are widely used for image processing.

To ensure the right data format is sent to the Conv1D layer, we first play a bit with arrays. Fortunately PyTorch allows immediate results, so here they are:

x = torch.tensor(
    [
        [1, 2, 3, 4, 5, 6, 7, 8],
        [1, 2, 3, 4, 5, 6, 7, 8],
        [1, 2, 3, 4, 5, 6, 7, 8],
    ], dtype=torch.float32)

x = torch.reshape(x, (x.shape[0], int(x.shape[1] / 2), 2)).permute(0, 2, 1)
print(x.numpy())

Outputting

[[[1. 3. 5. 7.]
  [2. 4. 6. 8.]]

 [[1. 3. 5. 7.]
  [2. 4. 6. 8.]]

 [[1. 3. 5. 7.]
  [2. 4. 6. 8.]]]

This is inline with our expectation that Conv1D operation will convolve along the time dimension. With this knowledge, we build our network.

class CNNRegressor(nn.Module):
    def __init__(self, in_channels, target_size):
        super().__init__()

        self.in_channels = in_channels

        self.seq_stack = nn.Sequential(
            nn.Conv1d(in_channels=in_channels, out_channels=256, kernel_size=5, padding='same'),
            nn.ReLU(),
            nn.AdaptiveAvgPool1d(output_size=8),
            nn.Flatten(),
            nn.Linear(256 * 8, 64),
            nn.ReLU(),
            nn.Linear(64, 64),
            nn.ReLU(),
            nn.Linear(64, target_size)
        )

    def forward(self, x):
        x = torch.reshape(x, (x.shape[0], int(x.shape[1] / self.in_channels), self.in_channels)).permute(0, 2, 1)
        return self.seq_stack(x)
    

t, v, tt = make_loaders(24, 1, 1)
model = CNNRegressor(t.dataset.count_channels(), t.dataset.get_target_size()).to(device)
print(model)
print("Total params: ", sum(p.numel() for p in model.parameters() if p.requires_grad))

CNNRegressor(
  (seq_stack): Sequential(
    (0): Conv1d(16, 256, kernel_size=(5,), stride=(1,), padding=same)
    (1): ReLU()
    (2): AdaptiveAvgPool1d(output_size=8)
    (3): Flatten(start_dim=1, end_dim=-1)
    (4): Linear(in_features=2048, out_features=64, bias=True)
    (5): ReLU()
    (6): Linear(in_features=64, out_features=64, bias=True)
    (7): ReLU()
    (8): Linear(in_features=64, out_features=1, bias=True)
  )
)
Total params:  156097

We immediately see the number of total parameters is smaller, even if I did no real tuning to the layer shapes, while the end results are not significantly different from the DNN. For this toy example, I did not expect much improvement.

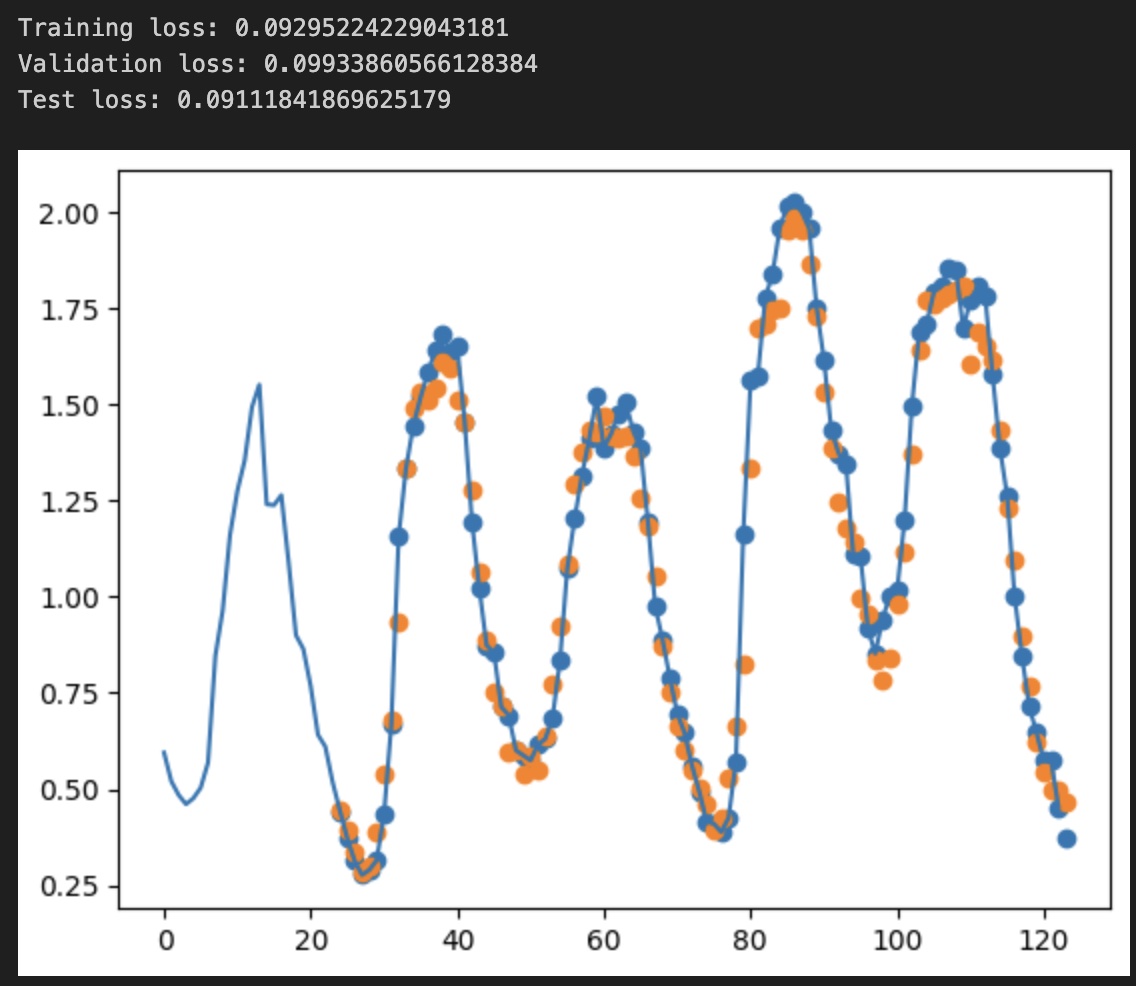
Recurrent Neural Network

I will finish my post by showing the same algorithm, but this time using RNNs. I will replace all the deep layers with 4 LSTM layers. We will notice a huge decrease (3x compared to the CNN) in the number model parameters, while keeping the same performance, even a notch better. To note the way data is transmitted to the LSTM block; again we make sure the series is sent to the network along the time axis.

class LSTMRegressor(nn.Module):
    def __init__(self, input_size, target_size):
        super().__init__()

        self.lstm = nn.LSTM(
            input_size=input_size, 
            hidden_size=input_size * 2, 
            num_layers = 4,
            batch_first = True)
        
        self.input_size = input_size # number of channels
        self.linear = nn.Linear(input_size * 2, target_size)

    def forward(self, x):
        seq_len = int(x.shape[1] / self.input_size)
        x = torch.reshape(x, (x.shape[0], seq_len, self.input_size)).permute(0, 1, 2)
        ret_lstm, (hn, cn) = self.lstm(x)
        lin_input = ret_lstm[:, -1, :] # take the last output from the sequence
        return self.linear(lin_input)
    

t, v, tt = make_loaders(24, 1, 1)
model = LSTMRegressor(input_size=t.dataset.count_channels(), target_size=t.dataset.get_target_size()).to(device)
print(model)
print("Total params: ", sum(p.numel() for p in model.parameters() if p.requires_grad))

LSTMRegressor(
  (lstm): LSTM(16, 32, num_layers=4, batch_first=True)
  (linear): Linear(in_features=32, out_features=1, bias=True)
)
Total params:  31777

The LSTM cells will memorize the most important features of th data, processing the input as a sequence passed through the network in one timestep at a time.

The results applying this network to the validation data, below:

Linear Regression and Timeseries

Using a statistical tools such as linear regression with time series can be problematic. Linear regression assumes you have independently and normally distributed data, while, in time series data, points near in time tend to be strongly correlated with one another. This is precisely the property that makes timeseries analysis important as, if there aren’t temporal correlations, it would be impossible to perform tasks such as predicting the future or understanding temporal dynamics.

Linear regression can be used with timeseries when linear regression assumptions hold, for instance when the predicted variable is fully dependent on its predictors and the errors preserve the normality assumption with no autocorrelation. In such a case, the timeseries element is entirely embedded in one of the features.

The Statistics Of Time Series

An excellent introduction on time series can be found here.

Timeseries bring several concepts of interest

• Stationarity: constant statistical properties of the timeseries (mean, variance, no seasonality)
• Self-correlation: correlation between subsequent values of a timeseries
• Seasonality: time-based patterns tha repeat at set intervals
• Spurious correlations: the propensity of timeseries to correlate with other unrelated timeseries especially when seasonality or trends are present.

A log transformation or a square root transformation are two usually good options for making a timeseries stationary,particularly in the case of changing variance over time.

Most of the timeseries have a trend, that is the mean is not constant - trend-stationarity and difference-stationarity. Removing a trend is most commonly done by differencing. Sometimes a series must be differenced more than once. However, if you find yourself differencing too much (more than two or three times) it is unlikely that you can fix your stationarity problem with differencing.

If v(t_i+1) - v(t_i) is random and stationary, then the process generating the series is a random walk, else a more refined model is required.

The test that is mainly used for testing stationarity is called the Augmented Dickey Fuller Test. It removes the autocorrelation and tests for equal mean and equal variance throughout the series. The null hypothesis is the non-stationarity.

The Dickey Fuller test assumes that the time series is an AR1 process (auto-regressive one), that is, it can be written as y(t) = phi * y(t-1) + constant + error. The DF test’s null hypothesis is phi >= 1. The alternate hypothesis is that phi < 1. This phi == 1 is called a unit root. A good explanation of unit roots can be found here.

ADF extends the test to ARn series and this null hypothesis is that sum(phi_i)>=1. The difference between the basic DF test and the ADF test is that the latter makes is to account for more lags. The test of whether a series is stationary is a test of whether a series is integrated. An integrated series of order n is a series that must be differenced n times to become stationary.

import random
from statsmodels.tsa.stattools import adfuller

def gen_ts(start, coefs, count, error):
  assert(len(start) == len(coefs))
  assert(count > len(start))

  lst = start + [0] * (count - len(start))

  for i in range(len(start), count):
    lst[i] = random.uniform(-0.5, 0.5) * error
    for j in range (1, len(start)+1):
      lst[i] += coefs[j-1] * lst[i-j]

  return lst

v = gen_ts([0, 1, 2], [0.5, 0.2, 0.1], 100, 1.0) # sum of coefficients < 1
plt.plot(v)

# automatically test for the best lag to use
# AIC comes from https://en.wikipedia.org/wiki/Akaike_information_criterion
p_value = adfuller(v, autolag='AIC')[1]
print(p_value)

For detecting auto correlation, we introduce two measures:

• The ACF - the autocorrelation between the value at t and t-n, including the intermediary values, (t-1 .. t-n-1). E.g. the effect of prices 2 months ago vs the prices today, including the effect of the prices 2 months ago on the prices 1 month ago and the prices from 1 month ago on today’s prices.
• The PACF - the autocorrelation between the value at t and t-n excluding the intermediary values.

The ACF is the Pearson correlation between the values ti and the lagged ti-k values. For the PACF we do a regression on the values of the timeseries at time ti on the ti-k of the form ti=phi_1*ti_-1 + phi_2*ti_-2 + ... + phi_k*ti_-k + error_term - autoregressive lag k. phi_k is our PACF(k).

To plot these a real dataset:

import pandas as pd

lynx_df = pd.read_csv("/content/drive/MyDrive/Datasets/LYNXdata.csv", 
    index_col=0, 
    header=0, 
    names=['year', 'trappings'])

And then transform it to time-annotated series:

lynx_ts = pd.Series(
    lynx_df["trappings"].values, 
    pd.date_range('31/12/1821', 
    periods=len(lynx_df), 
    freq='A-DEC'))

lynx_ts.plot()

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
plot_acf(lynx_ts, lags=100)
plot_pacf(lynx_ts, lags=10)

We see in these charts that autocorrelation decreases as we look backwards in the series. This means that we are likely dealing with an auto-regressive process. If we are to build an auto-regressive model for this series we’ll probably consider the coefficients for the 1, 2, 4 and 6 lags. The blue bands are the error margin; everything within the bands are not statistically significant. The coefficient with index 0 is always 1, as it is the correlation of the timeseries with itself.

A series can be stationary, that is the mean is 0 and the variance constant with time, but with no lag auto-correlation, no matter the lag value. Such a series is called white noise and it is not predictable.

Let’s plot some generated time series to explore the PCF and PACF charts for various cases.

white_noise = np.random.normal(0, 10, size=100)
plot_acf(white_noise)
plt.show()
plot_pacf(white_noise)
plt.show()

Let’s plot a perfect AR(1) model, with no noise.

# ar(1) process
ts2 = [white_noise[0]]
phi_0 = 10
phi_1 = 0.8
k = 0 # 0 = perfectly noiseless, 1 = very noisy

# Expected value of the timeseries (perfect timeseries converges to this value)
miu = phi_0 / (1-phi_1)
print("Expected value: ", miu)

for i in range(1, 100):
    # note that without the error term this goes fast to the mean
    # AR(1)
    ts2.append(phi_0 + ts2[i-1] * phi_1 + k * white_noise[i])

ts2 = np.array(ts2)
plt.plot(ts2)

plot_acf(ts2, lags=40)
plt.show()
plot_pacf(ts2, lags=40)
plt.show()

The time series converges to miu=phi_0 / (1-phi_1) = 50.

The same expected value can be observed if we increase the noise:

Now, let’s plot an MA (moving average) process:

ts3 = [white_noise[0]]
mean = 10
phi_1 = 0.8
for i in range(1, 100):
    # MA(1) - coef applied to the previous error
    ts3.append(mean + white_noise[i] + theta_1 * white_noise[i-1])

ts3 = np.array(ts3)
plt.plot(ts3)

plot_acf(ts3, lags=40)
plt.show()
plot_pacf(ts3, lags=40)
plt.show()

Unlike an autoregressive process, which has a slowly decaying ACF, the definition of the MA process ensures a sharp cutoff of the ACF for any value greater than q, the order of the MA process. This is because an autoregressive process depends on previous terms, and they incorporate previous impulses to the system, whereas an MA model, incorporating the impulses directly through their value, has a mechanism to stop the impulse propagation from progressing indefinitely. This also means that, forecasting beyond the value lag value of q will only return the mean, since there is no more noise to incorporate.

To summarize, when trying to identify what kind of model we try to fit, we have the following rules:

• AR(p) - ACF falls off slowly, PACF has sharp drop after lag = p
• MA(q) - ACF has a sharp drop after lag = q, PACF falls off slowly
• ARMA(p,q) - No sharp cutoff, neither for ACF nor for PACF

Fitting ARIMA Models

An ARIMA model has 3 parameters:

• p : the order of autoregression (the summation of the weighted lags) - AR
• d : the degree of differencing (used to make the dataset stationary if it is not) - I
• q : the order of moving average (the summation of the lags of the forecast errors) - MA

Examples (ARIMA(p, d, q)):

• ARIMA (p=1, d=0, q=0) <=> Y(t) = coef + phi_1 * Y(t-1) + error(t) - lag 1 autoregressive model
• ARIMA (p=1, d=0, q=1) <=> Y(t) = coef + phi_1 * Y(t-1) + theta_1 * error(t-1) + error(t) -
• ARIMA (p=0, d=1, q=0) <=> Y(t) = coef + Y(t-1) + error(t) is a random walk. The differencing equation, Y(t) - Y(t-1) = coef + error(t), is needed so that the remaining ARMA model is applied on stationary data. A random walk is not stationary.
• ARIMA(p=0, d=1, q=1) is an exponential smoothing model

ARIMA Model Parameter Selection

First step is to check for stationarity using the Augmented Dickey-Fuller test. If the data is not stationary, we need to set the d parameter.

The second step is to set the p and q parameters by inspecting the ACF and PACF plots, as described before.

To avoid over-fitting, a rule of thumb is to start the parameter selection with the plot that has the least amount of lags outside of the significance bands and then consider the lowest reasonable amount of lags. The ARIMA model is not necessary unique, as we will see in the following example where we start from a complex timeseries which can be approximated very well with a simpler model.

Let’s generate some data:

arma_series = [white_noise[0], white_noise[1]]
m = 5
phi_1 = 0.4
phi_2 = 0.3
theta_1 = 0.2
theta_2 = 0.2

# AR(2) I(0) MA(2)
for i in range(2, 100):
    arma_series.append( \
        m + \
        arma_series[i-1] * phi_1 + arma_series [i-2] * phi_2 + \
        white_noise[i] + theta_1 * white_noise[i-1] + theta_2 * white_noise [i-2])

plt.plot(arma_series)
plt.show()

adf = adfuller(arma_series, autolag='AIC')[1]
print(adf) # stationary

arma_series = np.array(arma_series)

# fit the model
plot_acf(arma_series)
plt.show()
plot_pacf(arma_series)
plt.show()

We observe a sharp cutoff in the PACF after lag 1 and slow decay in the ACF. This leads to try to fit an ARIMA(1, 0, 0).

from statsmodels.tsa.arima.model import ARIMA

m = ARIMA(arma_series, order=(1,0,0))
results = m.fit()
plt.plot(arma_series)
plt.plot(results.fittedvalues, color="orange")
print(results.arparams) # 0.78

A pretty good approximation of the initial complex model can be obtained with an AR(1) model. Let’s analyse the residuals to see how much information did we capture in our model and if there are autoregressive behaviors we have missed. In our case residuals are normally distributed as seen in the histogram and proven by the Shapiro test and in the ACF and PACF plots we do not see any autoregressive tendencies we might have missed.

resid = arma_series - results.fittedvalues
plt.hist(resid)

import scipy.stats as stats
# visual inspection of the residuals
plt.hist(resid)
# Shapiro test for normality
stats.shapiro(stats.zscore(resid))[1]

# no autocorrelation
plot_acf(resid)
plt.show()
plot_pacf(resid)
plt.show()

Returning to our Lynx timeseries which was shown earlier, let’s train an ARIMA model and see how it fits.

from statsmodels.tsa.arima.model import ARIMA
m = ARIMA(lynx_ts, order=([1], 0, 1))
results = m.fit()
plt.plot(lynx_ts)
plt.plot(results.fittedvalues, color="orange")
print(results.arparams)

Exported notebook is here

A good introductory video here

Simulated Annealing

Simulated annealing is an optimization algorithm used for solving complex problems where direct algorithmic solutions are hard to find. In cases where gradient descent cannot be used because the optimization function is not continuous we need a different approach, mostly based on trial and error. In such a situation, the solution is to make random moves in the solution space and only accept those moves that offer an optimization over the current state. However such moves can easily converge to a local optimum and get stuck. Therefore, a mechanism in needed to allow escape from the local optimum. Simulated annealing offers a solution to this problem allowing random non-optimal moves to be accepted with decreasing probability, based on a temperature schedule. The solution is borrowed from metalurgy where the steel is forged under slow cooling in order to allow for an optimal alignment of metal particles for increased durability.

For our problem the metric we want to optimize is the total length of the path. In the picture below you can see such a layout with a shortest path determined by the algorithm.

For the very same configuration we see the total path length plotted for each iteration.It is interesting to see the inflection point where, after settling on a higher length equilibrium, an local optimum, and a random move, the total length resettles to another, global optimum. We also see how fewer and fewer random moves are accepted, with lower and lower distance increase.

Solution Implementation

The full code is listed below. In short, we are computing the algorithm on a separate thread from the main rendering thread. The config can be reset by pressing ESC. You can add new points to the path by simply clicking somewhere on the screen. The distance evolution over each iteration can be displayed by pressing the P key.

The algorithm can be tuned by adjusting:

• The total number of iterations
• The temperature decay function
• The function for the probability of acceptance of a bad move

The algorithm has also a back step - if after accepting a bad move a better move is not found in a predefined number of steps, we backtrack to the best known configuration.

The move is made by randomly selecting two edges and switching their ends between themselves. Once the swap has been performed, in order fo maintain the path consistency, all edges between the two end points are inverted. This happens in the ComputeNewPath function.

package main

import (
	"GoAI/plt"
	"fmt"
	"github.com/tfriedel6/canvas/sdlcanvas"
	"math"
	"math/rand"
)

type Point struct {
	X float64
	Y float64
}

type Connection struct {
	Start int
	End   int
}

func (p *Point) Subtract(other *Point) Point {
	return Point{
		X: p.X - other.X,
		Y: p.Y - other.Y,
	}
}

func (p *Point) DistanceTo(other *Point) float64 {
	d := other.Subtract(p)
	return math.Sqrt(d.X*d.X + d.Y*d.Y)
}

type ConnsCollection struct {
	Points []Point
	Conns  []Connection

	// map ending to index in Conn
	endsIn []int
}

func (cc *ConnsCollection) BuildEndsInMap() {

	if cc.endsIn == nil || len(cc.endsIn) != len(cc.Conns) {
		cc.endsIn = make([]int, len(cc.Conns))
	}

	for i, cn := range cc.Conns {
		cc.endsIn[cn.End] = i
	}
}

func (cc *ConnsCollection) ComputeDistance() (float64, bool) {
	d := 0.0
	for _, c := range cc.Conns {
		if c.Start >= len(cc.Points) || c.End >= len(cc.Points) {
			return -1, false
		}
		d += cc.Points[c.Start].DistanceTo(&cc.Points[c.End])
	}
	return d, true
}

func (cc *ConnsCollection) DuplicateConnectionsTo(other **ConnsCollection) {

	if *other == nil {
		*other = &ConnsCollection{
			Points: cc.Points,
			Conns:  make([]Connection, len(cc.Conns)),
			endsIn: make([]int, len(cc.endsIn)),
		}
	}

	copy((*other).Conns, cc.Conns)
	copy((*other).endsIn, cc.endsIn)

}

func (cc *ConnsCollection) ComputeNewPath() float64 {

	conns := cc.Conns

	if len(conns) <= 1 {
		return 0.0
	}

	i1 := rand.Int() % len(conns)
	i2 := rand.Int() % len(conns)
	if i1 == i2 {
		i2++
		if i2 == len(conns) {
			i2 = 0
		}
	}

	p1 := &conns[i1]
	p2 := &conns[i2]

	// swap edges
	p1.End, p2.Start = p2.Start, p1.End

	for idx := p1.End; idx != p2.Start; {
		c := &conns[cc.endsIn[idx]]
		c.Start, c.End = c.End, c.Start
		idx = c.End
	}

	d, _ := cc.ComputeDistance()
	return d
}

func InitConnectionsFromPoints(points []Point) *ConnsCollection {

	c := ConnsCollection{
		Points: points,
		Conns:  make([]Connection, 0, 20),
	}

	// crate a path where each point is travelled only once
	for i := range c.Points {

		s := i
		e := i + 1

		if e == len(c.Points) {
			e = 0
		}

		c.Conns = append(c.Conns, Connection{
			Start: s,
			End:   e,
		})
	}

	c.BuildEndsInMap()

	return &c
}

func TravellingSalesman(in <-chan []Point, out chan<- *ConnsCollection) {

	for {

		// read all points and only start the computation once I finished points
		points := <-in
		for len(in) > 0 {
			points = <-in
		}

		var conns, conns2, resetPoint *ConnsCollection
		conns = InitConnectionsFromPoints(points)
		conns.DuplicateConnectionsTo(&conns2)
		conns.DuplicateConnectionsTo(&resetPoint)

		d, _ := conns.ComputeDistance()
		dReset := d
		MaxDriftFromGlobalMinimum := 10 * len(points)
		countSinceReset := MaxDriftFromGlobalMinimum

		MaxIterations := 100000
		distanceEvolution := make([]float64, MaxIterations)

		for i := 0; i < MaxIterations; i++ {

			temperature := 0.1 * float64(MaxIterations-i) / float64(MaxIterations)
			temperature = math.Pow(temperature, 5)

			// switch two nodes
			d2 := conns2.ComputeNewPath()

			// found a better move
			// or the temperature is high enough to accept other moves
			if d2 < d || (d2-d)*temperature > rand.Float64() {

				if d2 > d && i > (MaxIterations/100)*50 {
					fmt.Printf("Accepted bad move: iter: %v, temp: %v, distance: %v\n", i, temperature, d2-d)
				}

				conns2.BuildEndsInMap()
				conns2.DuplicateConnectionsTo(&conns)
				d = d2

				if d < dReset {
					dReset = d
					countSinceReset = MaxDriftFromGlobalMinimum
					conns2.DuplicateConnectionsTo(&resetPoint)
				}

			} else if countSinceReset < 0 {
				d = dReset
				countSinceReset = MaxDriftFromGlobalMinimum
				resetPoint.DuplicateConnectionsTo(&conns)
				resetPoint.DuplicateConnectionsTo(&conns2)
				//fmt.Println("Reset")
			} else {
				conns.DuplicateConnectionsTo(&conns2) // re-init conns2
			}

			countSinceReset--

			// save for analysis
			distanceEvolution[i] = d
		}

		plt.Reset()
		plt.LinePlot(distanceEvolution, "Distance Evolution", 1000)

		if d > dReset {
			out <- resetPoint
		} else {
			out <- conns
		}
	}
}

func main() {
	wnd, cv, err := sdlcanvas.CreateWindow(1280, 720, "Travelling Salesman")
	if err != nil {
		panic(err)
	}
	defer wnd.Destroy()

	points := make([]Point, 0, 10)
	connections := make([]Connection, 0, 10)
	distance := 0.0

	submitPoints := make(chan []Point, 100)
	receiveConnections := make(chan *ConnsCollection)

	go TravellingSalesman(submitPoints, receiveConnections)

	wnd.MouseDown = func(btn int, x int, y int) {
		// on mouse down add new points
		points = append(points, Point{
			X: float64(x),
			Y: float64(y),
		})

		// send the points to be computed
		submitPoints <- points
	}

	wnd.KeyDown = func(scancode int, rn rune, name string) {
		switch name {
		case "Escape":
			points = make([]Point, 0, 10)
			connections = make([]Connection, 0, 10)
			distance = 0.0
		case "KeyP":
			plt.Execute() // show plot only when key is pressed
		}
	}

	wnd.MainLoop(func() {

		select {

		case cc := <-receiveConnections:
			if dd, ok := cc.ComputeDistance(); ok {
				distance = dd
				connections = cc.Conns
				fmt.Printf("New paths with distance %f\n", distance)
			}

		default:

		}

		// background
		w, h := float64(cv.Width()), float64(cv.Height())
		cv.SetFillStyle("#000")
		cv.FillRect(0, 0, w, h)

		// circles
		cv.SetStrokeStyle("#FFF")
		cv.SetLineWidth(2)
		cv.SetFillStyle(255, 0, 0)

		for _, c := range connections {
			cv.BeginPath()
			cv.MoveTo(points[c.Start].X, points[c.Start].Y)
			cv.LineTo(points[c.End].X, points[c.End].Y)
			cv.Stroke()
		}

		for _, p := range points {
			cv.BeginPath()
			cv.Arc(p.X, p.Y, 10, 0, math.Pi*2, false)
			cv.ClosePath()
			cv.Fill()
			cv.Stroke()
		}

		cv.SetFont("Righteous-Regular.ttf", 12)
		cv.FillText(fmt.Sprintf("Total distance: %f", distance), 20, 20)

	})
}

Easy Charting From Go

Since I couldn’t find any charting library that met my needs, to be easy to use from a desktop application, I’ve decided to build my own. It relies on the excellent matplotlib library from python. The solution is simple: it generates a python script containing all the values I need to plot and, then, it launches that script in a separate process with its own window. For this we are using golang text templates to generate the script. I will extend the library for future use with other types of charts. Below you can see the code:

The template:

import matplotlib.pyplot as plt

 

values=
plt.plot(values)

 

plt.show()

The code for generating the template:

package plt

import (
	"fmt"
	"io/ioutil"
	"log"
	"os"
	"os/exec"
	"strings"
	"text/template"
)

type Plot struct {
	Type   string
	Values [][]float64
	Name   string
	Count  int
}

var plots []Plot = nil
var tmpl *template.Template = nil

func min(a int, b int) int {
	if a < b {
		return a
	} else {
		return b
	}
}

func compressByMean(count int, arr []float64) []float64 {

	ret := make([]float64, count)
	intvLen := len(arr) / count
	cnt := float64(intvLen)

	for i := 0; i < count-1; i++ {

		upperLimit := (i + 1) * intvLen
		lowerLimit := i * intvLen

		ret[i] = arr[lowerLimit] / cnt

		for j := lowerLimit + 1; j < upperLimit; j++ {
			ret[i] += arr[j] / cnt
		}
	}

	// last one is the last value - a hack for the simulated annealing problem
	ret[count-1] = arr[len(arr)-1]
	return ret
}

func toPythonArray(arr []float64) string {
	sb := strings.Builder{}
	sb.WriteString("[")

	for i, v := range arr {
		sb.WriteString(fmt.Sprintf("%f", v))
		if i < len(arr) {
			sb.WriteString(", ")
		}
	}

	sb.WriteString("]")
	return sb.String()
}

func init() {

	log.Println(os.Getwd())

	fn := template.FuncMap{
		"CompressByMean": compressByMean,
		"ToPythonArray":  toPythonArray,
	}

	tmpl = template.Must(template.New("chart_template.gopy").Funcs(fn).ParseFiles("chart_template.gopy"))
}

func LinePlot(arr []float64, name string, count int) {

	v := Plot{
		Type:   "line",
		Values: make([][]float64, 1),
		Name:   name,
		Count:  count,
	}

	v.Values[0] = arr
	plots = append(plots, v)
}

func Reset() {
	// clear the plots
	plots = nil
}

func Execute() {

	var fileName string

	func(fn *string) {
		f, err := ioutil.TempFile("./plots", "plt*.py")

		if err != nil {
			fmt.Println(err)
			return
		}

		defer f.Close()
		*fn = f.Name()

		if err := tmpl.Execute(f, plots); err != nil {
			log.Panic(err)
		}

		Reset()

	}(&fileName)

	go func(fileName string) {
		if out, err := exec.Command("python", fileName).Output(); err != nil {
			log.Println(err)
			log.Println(out)
		} else {
			log.Println(out)
		}
	}(fileName)

}

Testing

We will be building on the foundations laid in the previous blogpost. The code is on GitHub, here

To open and send commands to our WebSocket server, in Javascript Console, in any browser, you can do:

// connect to our websocket endpoint
let ret = new WebSocket("ws://localhost:8080/websocket")

// subscribe to changes to the first 1024 product IDs
req.send(JSON.stringify({command: "subscribe", productIDs: [...Array(1024).keys()]}))
req.onmessage = (msg) => console.log(msg)

Later, when we want to test the connection closing, do

req.close()

Meanwhile, from a different console, we will be performing POST, PUT and DELETE requests to change the products in the database. These requests are similar to the following:

POST http://localhost:8080/products
Content-Type: application/json

{
  "productId": 0,
  "manufacturer": "Apple",
  "pricePerUnit": "500EUR",
  "unitsAvailable": 6,
  "productName": "MacBook Pro"
}

Database Changes

In order to be able to listen to changes in the database, we will use the LISTEN / NOTIFY system from Postgresql. We are going to create a trigger which sends JSON messages whenever an update to the Products table occurs and we are going to initialize a listener in our service code to such events.

The trigger procedure below:

CREATE OR REPLACE FUNCTION notify_event_on_products_update() RETURNS TRIGGER AS $$
	DECLARE 
		data json;
		notif json;
	BEGIN
		IF (TG_OP = 'DELETE') THEN
			data = row_to_json(OLD);
		ELSE
			data = row_to_json(NEW);
		END IF;

		notif = json_build_object(
			'action', TG_OP,
			'product', data 
		);		
		PERFORM pg_notify('product_change', notif::text);
	
		RETURN NULL;
	END
$$ LANGUAGE plpgsql;

DROP TRIGGER IF EXISTS products_change_trigger ON products;

CREATE TRIGGER products_change_trigger AFTER INSERT OR UPDATE OR DELETE ON products
	FOR EACH ROW EXECUTE PROCEDURE notify_event_on_products_update();

Now, that we have this procedure, the code that listens to the emitted events, is listed below. It is invoked as a goroutine and acts as a backgorund service. It uses directly the pq package instead of the sql package because it relies on native Postgres functionality - the listen/notify mechanism.

// ListenForNotifications should be invoked as a goroutine
func ListenForNotifications(event string, notif func(json []byte)) error {

	listener := pq.NewListener(ConnectionString, 1*time.Second, 10*time.Second, 
	func(ev pq.ListenerEventType, err error) {
		log.Println(ev)
		if err != nil {
			log.Println(err)
		}
	})

	if err := listener.Listen(event); err != nil {
		return err
	}

	for {
		select {
		case n := <-listener.Notify:
			// updates
			notif([]byte(n.Extra))

		case <-time.After(90 * time.Second):

			log.Println("No events, pinging the connection")
			if err := listener.Ping(); err != nil {
				fmt.Println(err)
				return err
			}
		}
	}
}

The snippent which launches listening is in the main function,

go func() {
	if err := database.ListenForNotifications("product_change", 
		product.HandleChangeProductNotification); err != nil {
		log.Fatal(err)
	}
}()

The WebSocket Endpoint

First, initialize the route. Please notice the websocket package instead of the http used above.

func GetHTTPHandlers() map[string]http.Handler {
	return map[string]http.Handler{
		"/products":  http.HandlerFunc(productsHandler),
		"/products/": http.HandlerFunc(productHandler),
		// new handler for websocket
		// notice the websocket. package instead of the http.
		"/websocket": websocket.Handler(productChangeWSHandler),
	}
}

And then the handler itself. Its structure is straight forward:

• Exit the function when the connection closes.
• Register a cleanup sequence for when the connection finished.
• Launch a goroutine to listen to incoming messages and EOF error, signifing the connection closing.
• Loop in the same goroutine to send the relevant data to the client.

func productChangeWSHandler(ws *websocket.Conn) {

	// make the chan buffered so we can receive more messages until we process them
	inMsgChan := make(chan inMessage, 1024)
	inProductsUpdated := make(chan *Product, 1024)

	defer func() {
		addRemoveSubscription <- chanSubscriptionCmd{
			Cmd:      "closeconn",
			CommChan: inProductsUpdated,
		}

		// drain the channel
		for range inProductsUpdated {
		}

	}()

	go func(ws *websocket.Conn) {
		for {
			ws.MaxPayloadBytes = 1024 * 256
			var msg inMessage

			if err := websocket.JSON.Receive(ws, &msg); err != nil {
				log.Println(err)
				break
			}
			inMsgChan <- msg
		}
		close(inMsgChan)
	}(ws)

	for {
		select {
		case msg, ok := <-inMsgChan:
			// subscribe - unsubscribe
			if !ok {
				return // connection close
			} else {

				addRemoveSubscription <- chanSubscriptionCmd{
					Cmd:        msg.Cmd,
					ProductIDs: msg.ProductIDs,
					CommChan:   inProductsUpdated,
				}

			}
		case product, ok := <-inProductsUpdated:
			// updated products
			if !ok {
				return
			}

			if err := websocket.JSON.Send(ws, product); err != nil {
				log.Println(err)
				return
			}
		}
	}
}

The Algorithm

The algorithm is straight forward. It keeps a map of productIDs - channels listening for updates. When an update comes for a specific product ID, all the channels are notified. The interesting part is the use of goroutines for synchronization between processes. The map is local to a goroutine, which is launched as a service when the application starts, and all communications with it happen over channels. There is no shared memory involved and no shared-memory-specific synchronization primitives. The commented ode below.

A notable mention is the fact that clearing the subscription on connclose event is very slow as the function has to iterate through all the registered products. In a production scenario, I’d keep another map, a reversed index, so that I the relationship channel -> productID is faster to navigate. In our case it would have only make the code longer and less readable.

// shared channel on which the listen-notify db mechanism sends the products
var prodChan = make(chan productNotification, 1024)

// shared channel on which subscriptions are added / removed
var addRemoveSubscription = make(chan chanSubscriptionCmd)

func handleDistributionGoroutine() {

	// our map, product id -> channels
	// the second map is used because there is no Set in go
	notifyUpdates := make(map[int]map[chan *Product]bool)

	for {

		select {

		case incomingProduct := <-prodChan:

			notifChans, exists := notifyUpdates[incomingProduct.Product.ProductID]
			if exists && notifChans != nil {
				for k, v := range notifChans {
					if v {
				// this will block all threads in case of a single slow reader
				// the chan will fill and it will not be possible to send other
				// notifications to other readers.
				// option is to do launch each as a separate goroutine
				// but it will not guarantee order at the receiving side
						go func() { k <- &incomingProduct.Product }()
					}
				}
			}

		case subscription := <-addRemoveSubscription:

			switch subscription.Cmd {

			case "subscribe":
				for _, prd := range subscription.ProductIDs {
					ret, ok := notifyUpdates[prd]
					if !ok {
						ret = make(map[chan *Product]bool)
						notifyUpdates[prd] = ret
					}
					ret[subscription.CommChan] = true
				}
			case "unsubscribe":
				for _, prd := range subscription.ProductIDs {
					delete(notifyUpdates, prd)
				}

			case "closeconn":

				// empty the rest
				// we might wrap the following in a goroutine 
				// so we don't block futher incoming messages 
				emptyKeys := make([]int, 0, 100)

				for k, v := range notifyUpdates {
					delete(v, subscription.CommChan)
					if len(v) == 0 {
						emptyKeys = append(emptyKeys, k)
					}
				}
				// clear the map of empty keys
				for _, k := range emptyKeys {
					delete(notifyUpdates, k)
				}
				close(subscription.CommChan)

			default:
				log.Printf("Unhandled command %v", subscription.Cmd)
			}
		}
	}
}

// module init function to start the map service
func init() {
	go handleDistributionGoroutine()
}

HTTPS and HTTP/2

Before we launch to production our service, we need to make sure we secure it. In order to accept connections over HTTPS, we need to change our http.ListenAndServe invocation to http.ListenAndServeTLS and provide the call a certificate. We are going to generate ourselves such a certificate using generate_cert.go utility from the crypto/tls package.

The cert.pem file is the certificate with my public key inside while key.pem is my private key. When the session is established, a shared session key is generated by the client, signed with my public key. It is only I who can decode the shared key using my private key. The shared key is used to symmetrically encrypt messages

If I try to open now my service in Fireforx I get a security warning, but after I accept the warning I can access my service over https.

The nice thing about go is that, once I upgrade to HTTPS, I automatically upgrade to HTTP/2. This change comes for free and includes out-of-the-box features such as:

• Request multiplexing
• Header compression
• Security by default, since it is running over HTTPS
• Server push

From these, we will discuss a bit server push. What server push does is to send to the client assets which were not previously requested before they are requested. An example is when the browser requires index.html and we know that it is styled with main.css, append to the request this file also. This saves loading times and browser roundripts. A problem arises when the asset is cached with Cache-Control in which condition it will get pushed anyway, increasing the size of the request. A simple solution to this issue is to set a cookie when the page is visited and, if the cookie is present, do not send the asset with server push. If the cookie is present we can safely assume the browser has the asset already cached and, if not, it will be requested anyway when it encounters it.

Since not all connections have the ability to do server push, we need to check for this capability. In our handler we do:

func mySeverPushRequest(w http.ResponseWriter, r *http.Request) {

	// get the pusher interface out of our writer
	if pusher, ok := w.(http.Pusher); ok {

		if cookieAssetsPushed, err := r.Cookie("assetspushed"); err == nil {
			// set cookie and cache control for one hour
			pusher.Push("main.css", &http.PushOptions {
				Header: http.Header{ 
					"Content-Type": []string{"text/css"} ,
					"Cache-Control": []string{"max-age=3600"},
					}
			})

			// 1h expiration time
 			expiration := time.Now().Add(time.Hour)
        	cookie :=    http.Cookie{
				Name: 		"assetspushed",
				Value:		"true",
				Expires:	expiration,
			}
        	http.SetCookie(w, &cookie)
		}
	}

	// continue serving files or executing templates
	[.......................]
}

Listening to Incoming Requests

For building HTTP services, golang comes with all batteries included. There’s no need to install any additional package, everything is already available in the standard library. The APIs are straight forward and the code is short and fast.

package main

import (
	"log"
	"net/http"
)

func customEndpoint(w http.ResponseWriter, r *http.Request) {
	w.Write([]bytes("Hello World"))
	log.Println("Served.")
}

func main() {

	// a /custom endpoint
	http.HandleFunc("/custom", customEndpoint)

	// listen on localhost, port :8080
	if err := http.ListenAndServe(":8080", nil); err != nil {
		log.Fatal(err)
	}

}

Handling JSON

If we want to export a field from a structure to JSON, its name has to start with a capital letter, making it a public symbol. Otherwise it will be considered as private and it will not appear in the output string.

We use annotations, which are accessible at runtime through reflection, to specify how the field will be serialized. There is no space between json, : and the name. If we skip the annotation, the structure will be serialized with its fields as JSON fields.

import "encoding/json"

type Product struct {
	ProductID      int    `json:"productId"`
	Manufacturer   string `json:"manufacturer"`
	PricePerUnit   string `json:"pricePerUnit"`
	UnitsAvailable int    `json:"unitsAvailable"`
	ProductName    string `json:"productName"`
}

To serialize JSON we do the following:

if bytes, err := json.Marshal(&Product{
	ProductID:      0,
	Manufacturer:   "Apple",
	PricePerUnit:   "2500EUR",
	UnitsAvailable: 15,
	ProductName:    "MacBook Pro",
}); err == nil {
	log.Println("Successfully serialized to JSON")
} else {
	log.Println("Failed to serialize object")
}

To deserialize, the following:

product := Product{}
err = json.Unmarshal(serializedJSONString, &product)

if err != nil {
	log.Println("Could not unmarshal")
}

Handling of HTTP Verbs

A simple WebService, handling the GET method, returning a list of products from an in-memory structure.

package main

import (
	"encoding/json"
	"fmt"
	"log"
	"math/rand"
	"net/http"
)

// Product type
type Product struct {
	ProductID      int    `json:"productId"`
	Manufacturer   string `json:"manufacturer"`
	PricePerUnit   string `json:"pricePerUnit"`
	UnitsAvailable int    `json:"unitsAvailable"`
	ProductName    string `json:"productName"`
}

// some products stored in memory to play a bit
var products []*Product

// endpoint handler
func productsHandler(w http.ResponseWriter, r *http.Request) {

	switch r.Method {

	// handling the GET verb
	case http.MethodGet:
		jsonStr, err := json.Marshal(products)
		if err != nil {
			log.Println(err)
			w.WriteHeader(http.StatusInternalServerError)
		} else {
			w.Header().Set("Content-Type", "application/json")
			w.Write([]byte(jsonStr))
		}
	// everything else, not impemented
	default:
		w.WriteHeader(http.StatusNotImplemented)
	}
}

func main() {

	// init a few products in memory
	products = []*Product{}

	for i := 0; i < 10; i++ {
		products = append(products, &Product{
			ProductID:      i,
			Manufacturer:   "Apple",
			PricePerUnit:   fmt.Sprintf("%vEUR", (rand.Int()%10)*100+500),
			UnitsAvailable: rand.Int() % 15,
			ProductName:    "MacBook Pro",
		})
	}

	// handler
	http.HandleFunc("/products", productsHandler)

	if err := http.ListenAndServe(":8080", nil); err != nil {
		log.Fatal(err)
	}
}

And the output:

To create a new product, we update the switch block from above with the following:

case http.MethodPost:
	body, err := ioutil.ReadAll(
		&io.LimitedReader{ // ensure we don't get DoS
			R: r.Body,
			N: 1024})

	if err != nil {
		log.Println(err)
		w.WriteHeader(http.StatusBadRequest)
		return
	}

	product := Product{}
	err = json.Unmarshal(body, &product)

	if err != nil || product.ProductID != 0 {

		if err == nil {
			err = errors.New("ProductID should be 0 - if you know the ID, use PUT")
		}

		log.Println(err)
		w.WriteHeader(http.StatusBadRequest)
		return
	}

	// give them an increment
	// for now assume products are in incremental order, sorted
	// ensure safe to this data structure
	mtx.Lock()
	defer mtx.Unlock()

	if len(products) > 0 {
		product.ProductID = products[len(products)-1].ProductID + 1
	}

	products = append(products, &product)
	w.Header().Set("Location", fmt.Sprintf("/products/%v", product.ProductID))
	w.WriteHeader(http.StatusCreated)

To test the service we just do

$curl -D - -X POST -H "Content-Type: application/json" -d '{"productId" : 0, "manufacturer": "Microsoft", "productName": "MS Surface"}' localhost:8080/products

And we get the expected response back

HTTP/1.1 201 Created
Date: Sat, 16 Jan 2021 09:09:20 GMT
Content-Length: 0

What we are going to do now is to implement GET for a specific product ID and PUT for updating a specific ID.

To do this, we need a new handler which we add to the main function. This will match the trailing /.

// handler for GET id and PUT id
http.HandleFunc("/products/", productHandler)

The URLs that will go to this handler take the form http://localhost:8080/products/id. We are also going to structure a bit better the handler, so the error handling is factored out of the main function.

func productHandler(w http.ResponseWriter, r *http.Request) {

	retCode := func(w http.ResponseWriter, r *http.Request) int {

		pathSegments := strings.Split(r.URL.Path, "/products/")

		if len(pathSegments) != 2 {
			return http.StatusBadRequest
		}

		productID, err := strconv.Atoi(pathSegments[len(pathSegments)-1])

		if err != nil {
			return http.StatusBadRequest
		}

		product := findProductByID(productID)

		if product == nil {
			return http.StatusNotFound
		}

		switch r.Method {
		case http.MethodGet:

			mtx.RLock()
			defer mtx.RUnlock()

			jsonStr, err := json.Marshal(product)
			if err != nil {
				return http.StatusInternalServerError
			}

			w.Header().Set("Content-Type", "application/json")
			w.Write([]byte(jsonStr))

			return http.StatusOK

		case http.MethodPut:

			mtx.Lock()
			defer mtx.Unlock()

			body, err := ioutil.ReadAll(
				&io.LimitedReader{
					R: r.Body,
					N: 1024})

			if err != nil || json.Unmarshal(body, &product) != nil {
				return http.StatusBadRequest
			}

			// ensure ID stays the same
			product.ProductID = productID
			return http.StatusAccepted
		default:
			return http.StatusMethodNotAllowed
		}

	}(w, r)

	log.Println(r.Method, r.URL.Path)
	w.WriteHeader(retCode)

}